Sum of squares of chords to the points of a regular $n$-gon

The CSU math graduate students have started writing a really fun monthly math magazine for the department, featuring stories, mathematical tidbits, and puzzles collected from the department and slid under all the professors’ doors each month. It’s been a joy to read, and every month they have a “Problem of the Month’’ as well. This month’s problem was particularly fun:

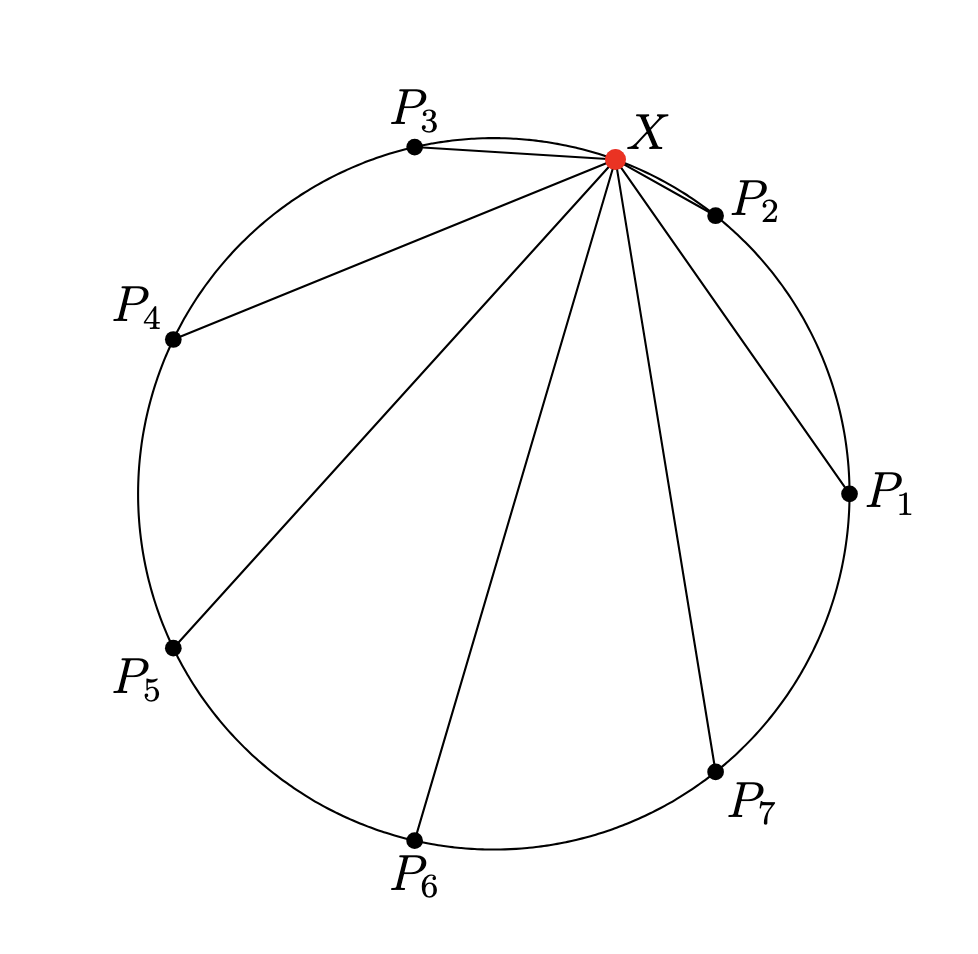
Let $P_1,P_2,\ldots,P_n$ be $n\ge 2$ points equally spaced around a circle of radius $r$, forming a regular $n$-gon. Let $X$ be any random point on the circle. Show that \(\|XP\_1\|^2+\|XP\_2\|^2+\\\cdots +\|XP\_n\|^2 = 2nr^2.\)

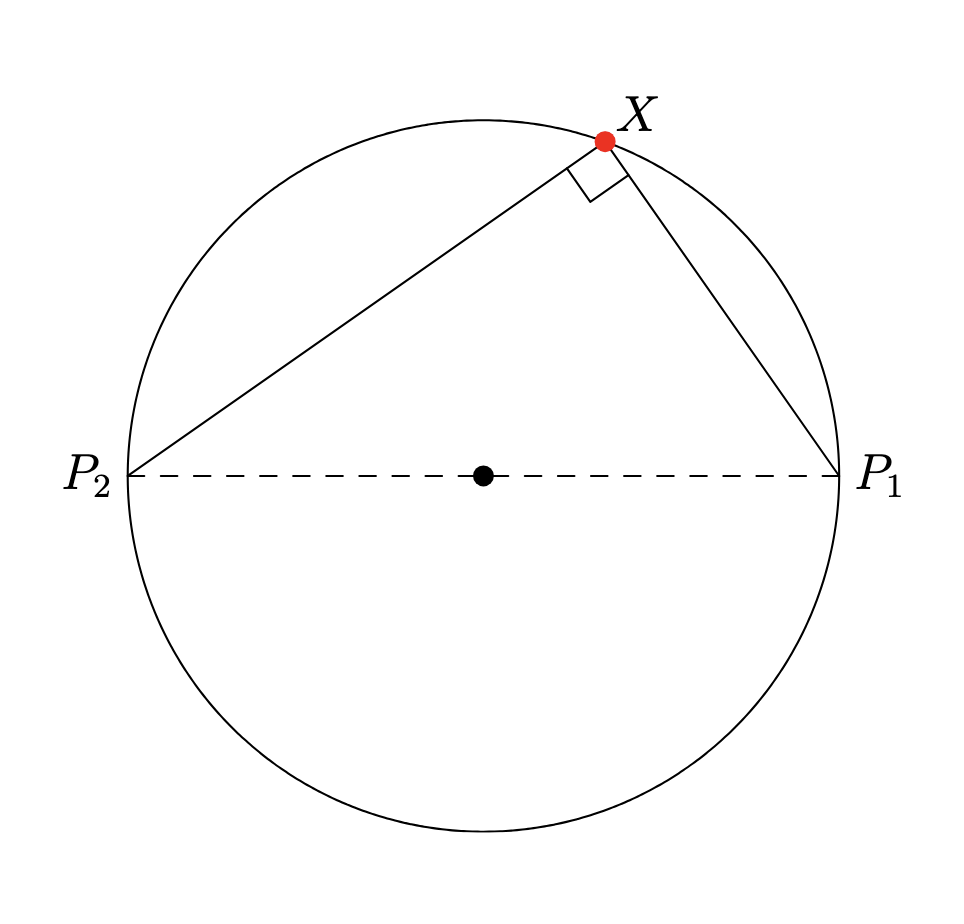
It’s fun to first prove this for $n=2$. In this case, the two chords $XP_1$ and $XP_2$ form a right angle because $P_1P_2$ is a diameter of the circle (and the angle spanning ). So by the Pythagorean theorem the sum of their squares is the square of the hypothenuse (diameter), which $(2r)^2=4r^2$, as desired:

How would you approach this? Here is a clean solution using complex numbers:

A note on the Schur-Zassenhaus theorem

I haven’t posted in a while; it’s time to dust off this blog and get things started again with a guest post!

In this post, guest user Anon1 posted a proof of the existence of finite fields of every possible order. Today I’ll share a writeup by the same user on the Schur-Zassenhaus Theorem in group theory!

The theorem statement

Let $G$ be a finite group, and let $N$ be a normal subgroup of $G$ such that $\gcd(|N|,[G:N])=1$. Then the Schur-Zassenhaus theorem says that:

1. $G$ has a subgroup $H$ such that $H \cong G/N$.
2. Any two such subgroups $H_1,H_2$ of $G$ are conjugate in $G$.

Recall that a subgroup $N$ is normal if $gNg^{-1}=N$ for all $g\in G$, and the quotient $G/N$ is the group of cosets $gN$.

An example

Let’s look at an example. In the symmetric group $S_3$, the alternating subgroup $A_3$ of odd permutations consists of the three cycles $(123)$ and $(132)$ along with the identity element, and is isomorphic to the cyclic group $C_3$. It has index $2$ in $S_3$, and $|A_3|=3$, and $2$ and $3$ are relatively prime, so the Schur-Zassenhaus theorem applies!

So $S_3$ should have a subgroup isomorphic to $C_2$, and indeed it does - it has three such subgroups in fact, those generated by the transpositions $(12)$, $(13)$, or $(23)$. These are indeed all conjugate to each other as well, by simply renaming the elements.

A nonexample

Can we do the same construction for $S_4$, or higher symmetric groups? The alternating group $A_4$ is still a normal subgroup, but now $|A_4|=12$ which is not relatively prime to $2$, the size of the quotient. So Schur-Zassenhaus does not apply. And indeed, not all of the subgroups of $S_4$ isomorphic to the quotient $C_2$ are conjugate to each other: The subgroup generated by $(12)$ is not conjugate to the subgroup generated by $(12)(34)$, since conjugation by permutations simply renames the letters in cycle notation!

The writeup and proof

User Anon1 sent me a full writeup of a proof of the first statement using affine geometry over fields of prime order, and it’s available here as a PDF at this link. Enjoy!

Hikita's proof of the Stanley-Stembridge Conjecture

In this arXiv paper, Hikita recently posted a proof of the famous Stanley-Stembridge conjecture! I went through the proof with my Advanced Combinatorics class, and wrote up lecture notes here:

Lecture Notes on Stanley-Stembridge Part I

Lecture Notes on Stanley-Stembridge Part II

which I will summarize in this post.

The Springer Correspondence Part IV: Affine Springer Fibers

I have written about the flag variety, the Springer resolution, and the relation between the type A Springer correspondence and Hall-Littlewood polynomials in a previous sequence of posts.

Time to extend this construction to the (type A) affine flag variety, corresponding to affine Lie type $\widetilde{A}_n$! We’ll also see how, due to a result of Hikita in 2012, this construction gives rise to a geometric interpretation of the famous symmetric functions $\nabla e_n$ from the Shuffle theorem.

How many trivalent trees does it take to hold up a moduli space?

After a bit of a hiatus due to difficulties with Wordpress, Mathematical Gemstones is back! Feel free to browse the new layout.

Today’s post introduces moduli spaces of curves, and one of the many ways combinatorial gemstones arise in this vast area of algebraic geometry.

A brief motivating question for studying families of curves: Given 4 general points in the plane, how can you write down all conics that pass through them? (Try it for the four points $(\pm 1, \pm 1)$!)