Pythagorean triples on a sphere?

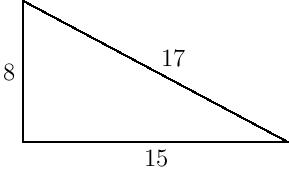
It’s 8/15/17, which means it’s time to celebrate! The three numbers making up the date today form a Pythagorean triple, a triple of positive integers $(a,b,c)$ with $a^2+b^2=c^2$. Indeed, $8^2+15^2=64+225=289=17^2$.

Alternatively, by the Pythagorean theorem, a Pythagorean triple is any triple of positive integers which make up the sides of a right triangle:

It’s exciting when all three sides are integers, since many common right triangles’ lengths involve square roots: $(1,1,\sqrt{2})$, $(1,2,\sqrt{5})$, and $(1,\sqrt{3},2)$, to name a few. And these sides aren’t even rational, which the poor Pythagorean scholar Hippasus discovered by proving that $\sqrt{2}$ is irrational and was subsequently drowned to death by his colleagues, according to some historical accounts. So the ancient Pythagoreans in fact only believed in right triangles having rational side lengths.

A faster divisibility rule for 7 (and 13)

I occasionally teach evening online classes for Art of Problem Solving (artofproblemsolving.com, a fantastic resource for high school students interested in learning mathematics), and one of the lessons I taught recently was on fast mental arithmetic tricks for testing divisibility by various small integers.

How do you tell if a number is divisible by $2$? Easy: look at the last digit. If that digit is even, the whole number is divisible by $2$, otherwise it’s not.

How do you tell if a number is divisible by $3$? Easy: Add up the digits and see if the sum is divisible by $3$. For instance, $1642$ is not divisible by $3$ because $1+6+4+2=13$ is not, but $1644$ is because $1+6+4+4=15$ is divisible by $3$.

The list goes on; there are nice, well-known divisibility rules for $4$, $5$, $6$, $8$, $9$, $10$, $11$, and $12$. But $7$ turns out to be rather annoying. Many of the existing texts on this subject use a recursive rule that goes something like this: Cross off the last digit, double that digit, and subtract it from the number that remains. Then keep doing that until you get a small number and see if the result is divisible by $7$.

Ouch.

Shifted partitions and the Orthogonal Grassmannian

In a previous post, we discussed Schubert calculus in the Grassmannian and the various intersection problems it can solve. I have recently been thinking about problems involving the type B variant of Schubert calculus, namely, intersections in the orthogonal Grassmanian. So, it’s time for a combinatorial introduction to the orthogonal Grassmannian!

What is the orthogonal Grassmannian?

In order to generalize Grassmannians to other Lie types, we first need to understand in what sense the ordinary Grassmannian is type A. Recall from this post that the complete flag variety can be written as a quotient of $G=\mathrm{GL}_n$ by a Borel subgroup $B$, such as the group of upper-triangular matrices. It turns out that all partial flag varieties, the varieties of partial flags of certain degrees, can be similarly defined as a quotient \[G/P\] for a parabolic subgroup $P$, namely a closed intermediate subgroup $B\subset P\subset G$.

Ellipses, parabolas, and infinity

A parabola can be defined as the locus of points equidistant from a fixed point (called the focus) and a fixed line (called the directrix). But we know from projective geometry that parabolas and ellipses are essentially the same object. Does this mean we can also define an ellipse in terms of a point and a line?

While tutoring a high school student recently, we worked through a problem that was essentially showing just that in a special case. Remarkably:

An ellipse can be defined as the locus of points $P$ for which the distance $|PF|$ to a focus $F$ is $\alpha$ times the distance from $P$ to a fixed line $\ell$ for some positive real number $\alpha\lt 1$.

Halloween Candy and Counting

Happy Halloween! It’s that time of year in which we celebrate ghosts, pumpkins, and fear itself. So, what better time to discuss a very common fear among adults these days: Mathematics!

If you’re reading this blog, I’m guessing you’re probably already not too afraid of mathematics. But I hope you share this post with people who are somewhat spooked by it but like to face their fears now and then. And let’s face it, even for math lovers, every difficult-sounding math problem is always a little scary at first… until you work it out and realize that there’s only beauty behind the mask.

I recently made up the following problem for a friend teaching a discrete mathematics class:

Five kids, dressed as a Ghost, a Witch, a Monster, a Skeleton, and a Black Cat, knock at your door. You open it and welcome them in, but you realize you only have $3$ Snickers bars and $3$ Kit Kats left in your candy stash!

Since you have $6$ pieces of candy and there are only $5$ kids, you decide to give both a Kit Kat and a Snickers bar to the scariest costume, and then give the remaining four kids one piece each. How many different ways can you choose who to give what candy to?