How many trivalent trees does it take to hold up a moduli space?
After a bit of a hiatus due to difficulties with Wordpress, Mathematical Gemstones is back! Feel free to browse the new layout.
Today’s post introduces moduli spaces of curves, and one of the many ways combinatorial gemstones arise in this vast area of algebraic geometry.
A brief motivating question for studying families of curves: Given 4 general points in the plane, how can you write down all conics that pass through them? (Try it for the four points $(\pm 1, \pm 1)$!)
We will come back to the above question, and how it ties in, in a future post. For now, some background: in previous posts, we’ve discussed moduli spaces of $k$-planes in $n$-dimensional space, called Grassmannians (see, for instance, the post on Schubert Calculus). In general, a moduli space is a geometric space whose points correspond to a family of geometric objects.
The moduli spaces $M_g$ (technically stacks, for higher genus) parameterize complex curves with genus $g$, and are a central object in algebraic geometry. In genus $0$, the combinatorial structure is particularly nice. Write $M_{0,n}$ for the moduli space of choices of $n\ge 3$ distinct labeled marked points $p_1,\ldots,p_n$ on the complex projective line $\mathbb{P}^1$, up to isomorphism.
Topologically, $\mathbb{P}^1$ over $\mathbb{C}$ is the surface of a sphere, even though we think of it as a complex “curve”, of dimension $1$ over $\mathbb{C}$. For instance, the image below shows a point of $M_{0,5}$.
Since a projective transformation of $\mathbb{P}^1$ is uniquely determined by where it sends three points, we can assume that the first three points have coordinates $0,1,\infty$ (or, in projective notation, $(0:1),(1:1),(1:0)$), and the remaining points can be any distinct points.
Compactification, stable curves, and dual trees
One natural compactification of this moduli space, $\overline{M}_{0,n}$, is called the space of stable curves, and essentially allows the distinct marked points to collide in the following way. When two points collide (like the two very close on the above picture), they form a new $\mathbb{P}^1$ that attaches to the original by a node at the point of collision, and the two points are now on the new $\mathbb{P}^1$. Since the new $\mathbb{P}^1$ only has three special points - the node and the two collided points - it does not matter, up to isomorphism, where these two points are placed on the new sphere:
In general, if multiple points collide, their coordinates on the new $\mathbb{P}^1$ will reflect the relative speeds at which the points approached the collision point along the chosen path in the moduli space.
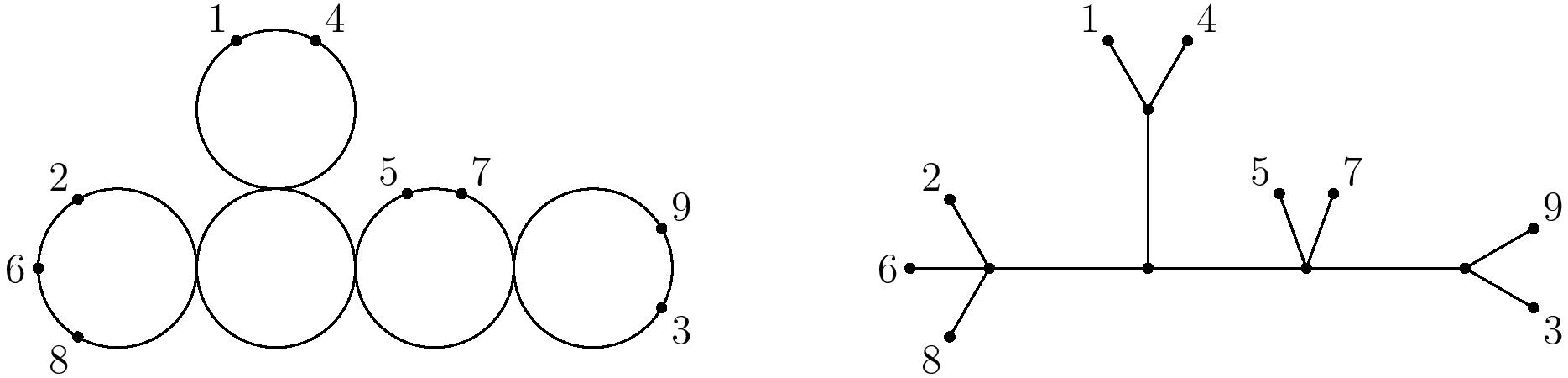
Simplifying the pictures somewhat so that we draw each $\mathbb{P}^1$ as a circle rather than a sphere (pretending visually that we are working over $\mathbb{R}$), in general a point of $\overline{M}_{0,n}$ can look like the diagram at left below, with each circle having at least three total special points (nodes or marked points).
The genus $g=0$ condition means that the $\mathbb{P}^1$’s are connected in a branching tree structure and do not loop around to form a necklace. This means that its dual graph is a tree - we draw one vertex for each $\mathbb{P}^1$ component and one for each marked point, and connect each component to its marked points and also to adjacent components. This forms the dual tree of a stable curve, shown at right above. These trees, by the stability condition, have the property that no vertex has degree $2$ (they are “at least trivalent”). The leaves are labeled and the internal vertices are unlabeled.
We now see a combinatorial object - trees - naturally arising in a moduli space of curves. In particular:
Trees play a similar role in $\overline{M}_{0,n}$ as partitions play in the Grassmannian, or permutations in the flag variety.
In particular, $\overline{M}_{0,n}$ has a boundary stratification given by the at-least-trivalent trees $T$ on $n$ labeled leaves, where $X_T$ is defined to be the closure of the set of all stable curves with dual tree $T$. These strata have a natural combinatorial condition for compatibility: $X_T$ is contained in $X_S$ if and only if the tree $T$ can be formed by contracting some of its edges to form $S$.
The smallest such strata are the boundary points $X_T$ where $T$ is a trivalent tree in which each internal vertex has exactly degree $3$. In this case, there is only one curve up to isomorphism with this dual tree, so the entire stratum is literally a single point in the moduli space.
We finally arrive at today’s gemstone: the enumeration of the boundary points in $\overline{M}_{0,n}$!
Boundary points and the double factorial
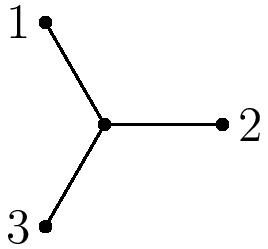
How many boundary points does $\overline{M}_{0,n}$ have? This is equivalent to enumerating the trivalent trees on $n$ labeled leaves. For $n=3$, there is only one such tree:
For $n=4$, there are three:
and notice that each of these three can be formed by attaching a leaf edge with its leaf vertex labeled $4$ to the midpoint of one of the three edges of the $n=3$ tree. Notice also that by inserting a leaf edge attached to the midpoint of an existing edge, the total number of edges in the tree increases by $2$. Moreover, any trivalent tree on leaves labeled $1,2,\ldots, n+1$ comes from a unique tree on $n$ leaves in this way, by deleting the leaf labeled $n+1$ and the edge it is a vertex of.
By induction, we conclude that there are $2n-3$ edges in any trivalent tree with $n$ labeled leaves, and if $T_n$ is the number of trivalent trees on $n$ labeled leaves, we have \[T_{n+1}=(2n-3) T_{n}\]. Starting from the base case $T_3=1$, we conclude that \[T_{n}=1\cdot 3 \cdot 5 \cdot 7 \cdot \cdots \cdot (2n-5)=(2n-5)!!\] Here the notation $(2n-5)!!$ denotes the double factorial, the product of the odd numbers up to $2n-5$. So for instance, $\overline{M}_{0,5}$ has $1\cdot 3 \cdot 5=15$ boundary points, and $\overline{M}_{0,6}$ has $7!!=105$. A beautiful gemstone of combinatorics within geometry!