Deriving the discriminant of a cubic polynomial through analytic geometric means
This is a contributed gemstone, written by Sushant Vijayan. Enjoy!
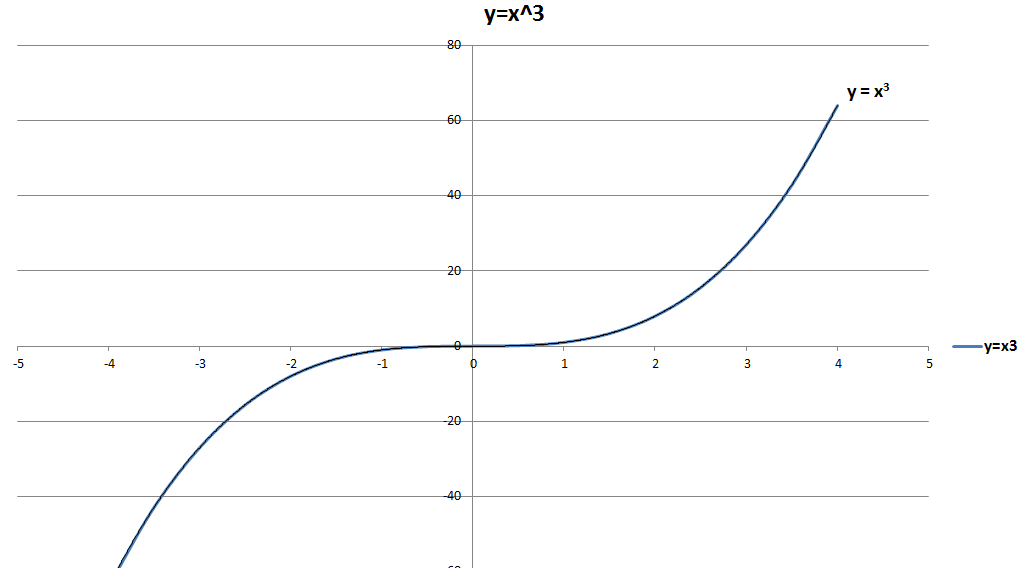
Consider a generic cubic equation \[at^3+bt^2+ct+d=0,\] where $a,b,c,d$ are real numbers and $a \neq 0$. Now we can transform this equation into a depressed cubic equation, i.e., one with no $t^2$ term, through means of Tschirnhaus Transformation $t=x-\frac{b}{3a}$, followed by dividing through by $a$. The depressed cubic equation is given by \[x^3+px+q=0\] where $p$ and $q$ are related to $a,b,c,d$ by the relation given here. Setting $p=-m$ and $q=-n$ and rearranging we arrive at \[x^3 =mx+n \hspace{3cm} (1)\] We will investigate the nature of roots for this equation. We begin with plotting out the graph of $y=x^3$:
The Springer Correspondence, Part III: Hall-Littlewood Polynomials
This is the third post in a series on the Springer correspondence. See Part I and Part II for background.
In this post, we’ll restrict ourselves to the type A setting, in which $\DeclareMathOperator{\GL}{GL}\DeclareMathOperator{\inv}{inv} G=\GL_n(\mathbb{C})$, the Borel $B$ is the subgroup of invertible upper triangular matrices, and $U\subset G$ is the unipotent subvariety. In this setting, the flag variety is isomorphic to $G/B$ or $\mathcal{B}$ where $\mathcal{B}$ is the set of all subgroups conjugate to $B$.
The Hall-Littlewood polynomials
For a given partition $\mu$, the Springer fiber $\mathcal{B}_\mu$ can be thought of as the set of all flags $F$ which are fixed by left multiplication by a unipotent element $u$ of Jordan type $\mu$. In other words, it is the set of complete flags \[F:0=F_0\subset F_1 \subset F_2 \subset \cdots \subset F_n=\mathbb{C}^n\] where $\dim F_i=i$ and $uF_i=F_i$ for all $i$.
Can you <i>prove</i> it?
As this ingenious post over at Math With Bad Drawings explained so clearly recently, there is a big difference between finding the answer to a math problem and being able to explain, beyond all reasonable doubt, why your answer is correct. It is the difference between solving it and proving it!
While mathematical proof is a huge part of math and science, it is unfortunately somewhat overlooked in the standard US curriculum. Partly for this reason, my family and I started a new math summer camp called Prove it! Math Academy. This year’s program will be a two-week crash course in proofs, using challenging problems and advanced mathematical concepts as examples.
Consider the following diagram which appears on our program website:
No explanation, no words, no proof. Just the picture. Enticing!
The Springer Correspondence, Part II: The Resolution
This is a continuation of The Springer Correspondence, Part I. Here we will work with unipotent matrices to construct the Springer resolution and the cohomology of its fibers.
Unipotent Matrices and Partitions
A unipotent element of a linear algebraic group $G$ is any element $u\in G$ such that $1-u$ is nilpotent. That is, $u=1+n$ where $n^k=0$ for some $k$.
To get a sense of what unipotent matrices look like, consider the type A situation in which $\DeclareMathOperator{\GL}{GL}\newcommand{\CC}{\mathbb{C}} G=\GL_n(\CC)$. Given a unipotent element $u$, we can conjugate it by some matrix to put it in Jordan normal form. It will look something like this: \[gug^{-1}=\left(\begin{array}{ccccccc} \lambda_1 & 1 & & & & & \\ & \lambda_1 & 1 & & & & \\ & & \lambda_1 & & & & \\ & & & \lambda_2 & 1 & & \\ & & & & \lambda_2 & & \\ & & & & & \ddots & \\ & & & & & & \lambda_k \end{array}\right)\]
The Springer Correspondence, Part I: The Flag Variety
In prior posts, we’ve seen that the irreducible representations of the symmetric group $S_n$ are in one-to-one correspondence with the partitions of $n$, and the Schur functions give an elegant encoding of their characters as symmetric polynomials. Now we can dive a bit deeper: a geometric construction known as the Springer resolution allows us to obtain all the irreducible representations of $S_n$ geometrically, and as a side bonus give natural graded representations that will allow us to define a $q$-analog of the Schur functions known as the Hall-Littlewood polynomials.
Quite a mouthful of terminology. Let’s start at the beginning.