PhinisheD!

Sometimes it’s the missteps in life that lead to the greatest adventures down the road.

For me, my pursuit of a Ph.D. in mathematics, specifically in algebraic combinatorics, might be traced back to my freshman year as an undergraduate at MIT. Coming off of a series of successes in high school math competitions and other science-related endeavors (thanks to my loving and very mathematical family!), I was a confident and excited 18-year old whose dream was to become a physicist and use my mathematical skills to, I don’t know, come up with a unified field theory or something.

But I loved pure math too, and a number of my friends were signed up for the undergraduate Algebraic Combinatorics class in the spring, so my young ambitious self added it to my already packed course load. I had no idea what “Algebraic Combinatorics” even meant, but I did hear that it was being taught by Richard Stanley, a world expert in the area. How could I pass up that chance? What if he didn’t teach it again before I left MIT?

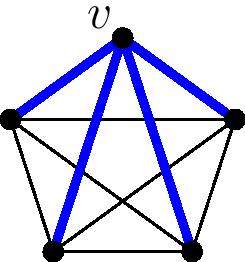
On the first day of the class, Stanley started with a simple combinatorial question. It was something like the following: In a complete graph with $n$ vertices, how many walks of length $k$ starting at vertex $v$ end up back at vertex $v$ on the last step? For instance, if $n=5$ and $k=2$, the graph looks like:

and there are four closed walks of length two, from $v$ to any other vertex and back again:

There is an elementary (though messy) way to solve this, but Stanley went forth with an algebraic proof. He considered the adjacency matrix $A$ of the complete graph, and showed that the total number of loops of length $k$ starting from any vertex is the trace of $A^k$. One can then compute this trace using eigenvalues and divide by $n$ to get the number of loops starting at $v$. Beautiful!

I remember sitting in my seat, wide-eyed, watching Richard Stanley quietly but authoritatively discuss the technique. It was incredible to me that advanced tools from linear algebra could be used to so elegantly solve such a simple, concrete problem. To use a term from another area of algebraic combinatorics, I was hooked.

But I was also a freshman, and didn’t yet have a strong grasp of some of the other algebraic concepts being used in the course. I studied hard but wound up with a B+ in the class. Me, get a B+ in a math class? I was horrified, my 18-year-old Little-Miss-Perfect confidence shattered. Now, not only was I fascinated with the subject, I gained respect for it. It was a worthy challenge, and I couldn’t help but come back for more.

In the years that followed, I took more courses on similar subjects and wrote several undergraduate research papers. I dabbled in other areas as well, but was always drawn back to the interplay between combinatorics and algebra. I now find myself, as of Friday, May 20, 2016, having completed my Ph.D. at UC Berkeley on a topic in algebraic combinatorics…

…and I often wonder how much that silly little B+ motivated me throughout the years.

My full thesis can be found here.

At Berkeley, my work mostly focused on the theory of symmetric functions, a central tool in algebraic combinatorics. Indeed, the schur functions alone enable us to work with the representations of $S_n$, the representations of $\mathrm{GL}_n$, and the cohomology of the Grassmannian, all from a combinatorial standpoint. With symmetric functions, we have turned many complex problems in algebra into the combinatorics of numbers written in boxes, better known as Young tableaux.

But all good combinatorial theories require an equally good $q$-analog, so naturally it doesn’t stop there. The Hall-Littlewood polynomials $\widetilde{H}_\mu(X;t)$ are a $t$-analog of the homogeneous symmetric functions $h_\mu$, which are Schur positive in the sense that their coefficients in the Schur basis are polynomials in $t$ with positive integer coefficients. Their associated graded $S_n$-module arises in the Springer resolution of the nilpotent cone in $\mathrm{gl}_n$, and are a particular subcollection of the LLT polynomials as well.

The combinatorics of Hall-Littlewood polynomials is now fairly well-understood, now that Lascoux and Schutzenberger coming up with the elusive cocharge statistic. But there is a further $q$-analog of the Hall-Littlewood polynomials, a class of polynomials called the Macdonald polynomials, that are not yet as well understood.

The Macdonald polynomials $\widetilde{H}_\mu(X;q,t)$ were first defined (in a slightly different form) by Ian Macdonald in his book Symmetric Functions and Hall Polynomials, which is now often referred to in algebraic combinatorics circles as the ``bible of symmetric function theory’’. He defined them as the eigenfunctions of certain linear operators, and showed that they are the unique symmetric functions satisfying certain orthogonality conditions with respect to a generalization of the Hall inner product. He also conjectured that they were Schur positive (the coefficients being polynomials in $q$ and $t$ over the positive integers), but didn’t have any particular reason why this should be so.

My advisor, Mark Haiman, showed that the Macdonald polynomials were Schur positive by showing that they are the characters of certain bi-graded representations of $S_n$ arising from the geometry of the Hilbert scheme of $n$ points in $\mathbb{C}^2$. Later, Haiman along with Jim Haglund and Nick Loehr came up with a combinatorial formula for the Macdonald polynomials; however, this formula does not easily imply Schur positivity in a combinatorial manner. Indeed, the formula is as follows:

\[\widetilde{H}_\mu(X;q,t)=\sum_{\sigma:\mu\to \mathbb{Z}_+} q^{\mathrm{inv}(\sigma)}t^{\mathrm{maj}(\sigma)} x^\sigma.\]

Here, the sum ranges over all fillings $\sigma$ of the Young diagram of $\mu$ with positive integers (with no other restrictions on the entries). The factor $x^\sigma$ denotes the monomial $x_1^{m_1(\sigma)}x_2^{m_2(\sigma)}x_3^{m_3(\sigma)}\cdots$ where $m_i(\sigma)$ is the number of times the number $i$ is used in the filling $\sigma$. The functions $\mathrm{inv}$ and $\mathrm{maj}$ are statistics on fillings that generalize the classical $\mathrm{inv}$ and $\mathrm{maj}$ statistics on permutations.

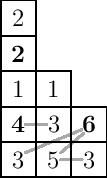
To calculate $\mathrm{maj}$, we calculate the major index of each column and add up the results. For instance, in the example below, the column words are $22143$, $135$, and $63$. The first has descents (shown in boldface in the diagram) in positions $2$ and $4$ from the left and therefore has major index $6$, the second has no descents, and the third has a descent in position $1$, so the total major index is $6+1=7$.

To calculate $\mathrm{inv}$, we count the number of relative inversions, defined as a pair of entries $u$ and $v$ in the same row, with $u$ to the left of $v$, such that if $b$ is the entry directly below $u$, one of the following conditions is satisfied:

• $u\lt v$ and $b$ is between $u$ and $v$ in size, in particular $u\le b\lt v$,
• $u\gt v$ and $b$ is not between $u$ and $v$ in size, in particular either $b\lt v\lt u$ or $v\lt u\le b$.

If $u$ and $v$ are on the bottom row, we treat $b$ as $0$. In the example above, there are two relative inversions: $(5,3)$ in the bottom row, and $(3,6)$ in the second, so $\mathrm{inv}(\sigma)=2$.

There is also another way to calculate $\mathrm{inv}$: define an attacking pair to be a bigger number followed by a smaller number in reading order, such that the smaller number is either directly to the right of the bigger or in the row just below it and to the left. The attacking pairs are shown by gray lines in the figure above. Then the $\mathrm{inv}$ is equal to the number of attacking pairs minus the total number of boxes to the right of each (boldfaced) descent. (Try it!)

The $\mathrm{inv}$ statistic in particular is quite complicated, and makes it difficult to work with the combinatorial formula to prove things like Schur positivity directly. It would be nice, in fact, if it was more like the $\mathrm{maj}$ statistic. But in a sense, we already know it must be like the $\mathrm{maj}$ statistic, because the geometric connection to the Hilbert scheme implies the following (conjugate) $q,t$-symmetry: \[\widetilde{H}_\mu(X;q,t)=\widetilde{H}_{\mu^\ast}(X;t,q).\]

Here $\mu^\ast$ is the conjugate partition, formed by reflecting the Young diagram about the main diagonal. This implies that $\mathrm{inv}$ and $\mathrm{maj}$, like their classical counterparts, exhibit a type of equidistribution on fillings. Indeed, there should exist a bijection from fillings of $\mu$ to fillings of $\mu^\ast$ that preserves the content and interchanges $\mathrm{inv}$ and $\mathrm{maj}$ simultaneously. And yet no such bijection is known.

I attempted to find such a bijection, and generalized the classical Carlitz bijection to a number of special cases. The main results of my thesis can be summarized as follows:

Theorem. The bijective maps $\mathrm{invcode}$ and $\mathrm{majcode}$ that comprise the Carlitz bijection $\mathrm{majcode}\circ\mathrm{invcode}^{-1}:S_n\to S_n$ can be extended to give bijections on fillings that interchange $\mathrm{inv}$ and $\mathrm{maj}$ in the following cases:

1. In the Hall-Littlewood specialization $q=0$, i.e. when one of the statistics is zero, for all partitions $\mu=(\mu_1,\mu_2,\mu_3)$ having at most three parts, and when $\mu=(a,b,1,1,\ldots,1)$ is the union of a column and a two-row shape.
2. In the Hall-Littlewood specialization $q=0$ (for all shapes) when we restrict to the fillings having distinct entries.
3. In the specialization $t=1$, i.e.~when one of the statistics is ignored.
4. When $\mu$ is a hook shape.

See the full thesis for the details on these crazy and fun bijections. Some of these results ended up giving rise to new recursive structures on the cocharge statistic and other interesting new directions to explore, particularly on Hall-Littlewood polynomials. But perhaps the most significant part of these results is that we are able to understand the symmetry, even if just in the Hall-Littlewood case, for three-row shapes. Three rows is notoriously difficult to understand in this area, with many partial results being published for two-row shapes, where $\mathrm{inv}$ is not yet very complicated, and getting stuck when one tries to move up to three rows.

Naturally, there is much work yet to be done. If there’s anything I’ve learned from my five years in graduate school, it’s that a Ph.D. is not a journey to an end, it’s the preparation for a beginning.

Thanks to…

No summary of my thesis would be complete without acknowledging the many people that have helped me along the way. My thesis is dedicated to my father, mother, and two brothers, who all helped make my childhood a wonderful and superbly educational one.

As for the other acknowledgments, below I have copied the acknowledgments page, since I feel people may be more likely to read it here than in the 94-page thesis document itself. (I can also provide links to some of their awesome web pages!)

I could not have completed this work without the patient and insightful guidance of my advisor, Mark Haiman. For the last five years, one Yali’s Cafe session at a time, he has taught me the secrets of the world of symmetric functions, Macdonald polynomials, diagonal harmonics, Hilbert schemes, and countless other topics. I am very grateful for his eagerness to talk about mathematics at any time, for his frank assessment of the significance of my results, and for giving me the freedom to choose my own directions in my research while also providing guidance along the way.

There are many other people who I am indebted to as well. I thank Sami Assaf and Angela Hicks for their generous insights on parking functions, quasisymmetric functions, and Macdonald positivity, and more generally for our many collaborative discussions. Sami and Angela have become like mathematical older sisters to me, and I am grateful for their advice and inspiration.

I thank Steven Sam for co-organizing a seminar on Macdonald polynomials with me in my second year of graduate school, without which I would have had a harder time learning the material. I also thank Monica Vazirani for being involved with that seminar, and more generally for her help throughout my graduate studies.

I thank Anne Schilling for suggesting potential new connections of this work to representation theory and crystal base theory, and I look forward to working with her on these connections in the future.

I also thank (in no particular order) Adriano Garsia, Jonah Blasiak, Jim Haglund, Andy Wilson, Sara Billey, and Austin Roberts for insightful discussions pertaining directly to this work. Thanks also to Federico Castillo, Steven Karp, Olya Mandelshtam, Anastasia Chavez, Lauren Williams, Thomas Lam, Jake Levinson, David Harden, and Allen Knutson for in-depth mathematical discussions on related topics throughout my studies at Berkeley. Thanks to Mark Haiman, Lauren Williams, and Christos Papadimitriou for serving on my dissertation committee.

Finally, I thank my husband, Bryan Gillespie, for being by my side for the last wonderful four years, and providing stability through the ups and downs of mathematical research.