Sum of squares of chords to the points of a regular $n$-gon

The CSU math graduate students have started writing a really fun monthly math magazine for the department, featuring stories, mathematical tidbits, and puzzles collected from the department and slid under all the professors’ doors each month. It’s been a joy to read, and every month they have a “Problem of the Month’’ as well. This month’s problem was particularly fun:

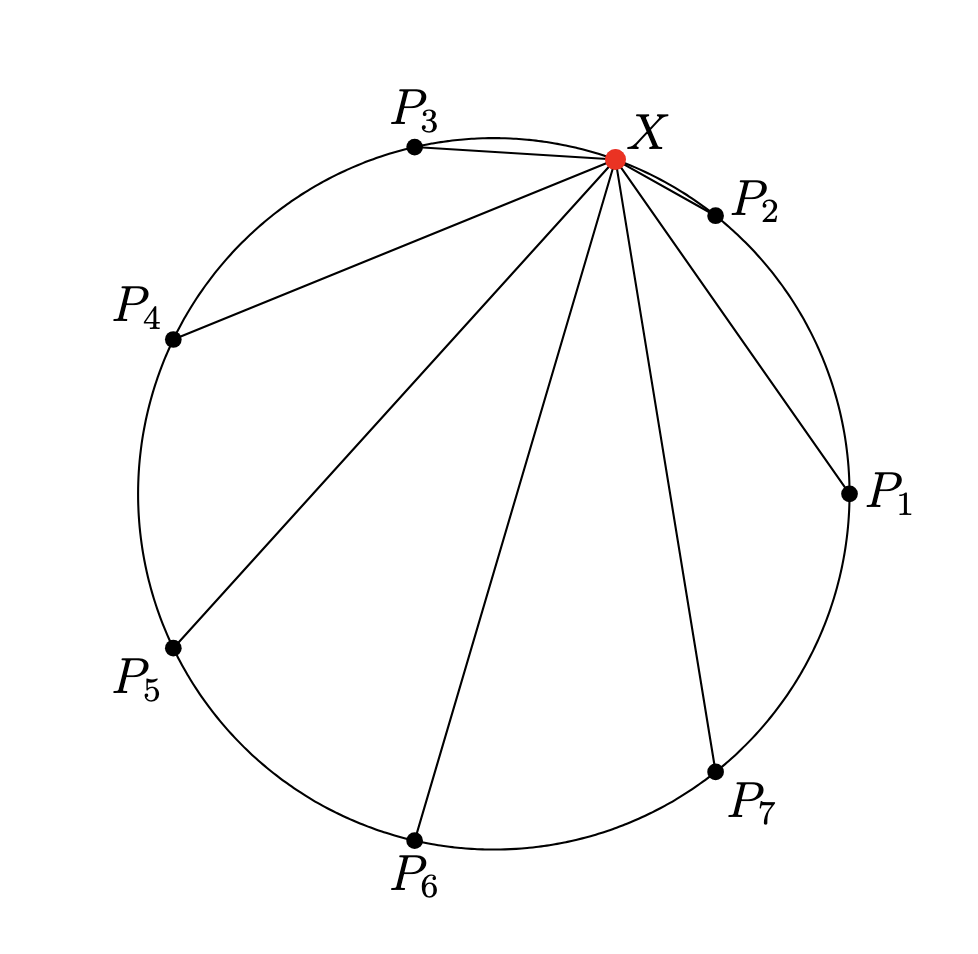
Let $P_1,P_2,\ldots,P_n$ be $n\ge 2$ points equally spaced around a circle of radius $r$, forming a regular $n$-gon. Let $X$ be any random point on the circle. Show that \(\|XP\_1\|^2+\|XP\_2\|^2+\\\cdots +\|XP\_n\|^2 = 2nr^2.\)

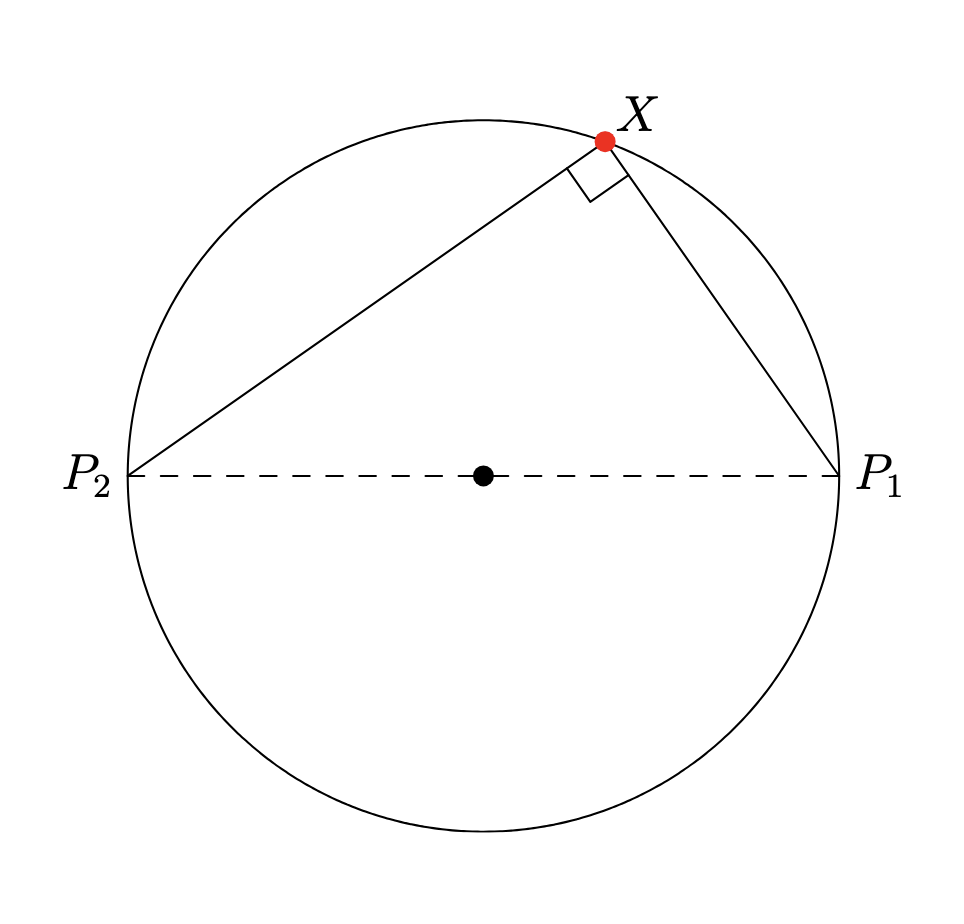
It’s fun to first prove this for $n=2$. In this case, the two chords $XP_1$ and $XP_2$ form a right angle because $P_1P_2$ is a diameter of the circle (and the angle spanning ). So by the Pythagorean theorem the sum of their squares is the square of the hypothenuse (diameter), which $(2r)^2=4r^2$, as desired:

How would you approach this? Here is a clean solution using complex numbers:

Let’s first scale everything by $1/r$, which also scales the squares of the chord lengths by $1/r^2$. Then we can assume our circle is a unit circle (of radius $1$), and we wish to show the sum of the squares of the chord lengths from $X$ to each $P_i$ is simply $2n$.

Now let’s center the circle at the origin in the complex plane, and rotate it so that point $P_1$ is at $1$. Then we can write $X=e^{i\theta}$ for some angle $\theta$, and $P_k=e^{2\pi i k/n}$ for all $k$. Then using the complex numbers facts that $|z|=z\overline{z}$ and $\overline{e^{i\theta}}=e^{-i\theta}$, the sum becomes

\[\begin{align} \sum_i |e^{i\theta}-e^{i2\pi k/n}|^2 & = \sum_i (e^{i\theta}-e^{i2\pi k/n})(e^{-i\theta}-e^{-i2\pi k/n}) \\ &= \sum_i 1+1-e^{i\theta}e^{-i2\pi k/n}-e^{-i\theta}e^{i2\pi k/n} \\ &= 2n - e^{i\theta}\sum_i e^{-i2\pi k/n} - e^{-i\theta} \sum_i e^{i2\pi k/n} \\ &= 2n - 0 - 0 \end{align}\]

where the last two sums are $0$ because they are the sum of the $n$ roots of unity around the circle, which are equally distributed and cancel as vectors. (This can also be shown using the finite geometric series formula to simplify the sum to $0$).

Very elegant problem, and a beautiful result!